|
|
|
 Description of optical fields with interesting distributions of intensity, phase, and/or polarization, both from the ray and wave points of view.
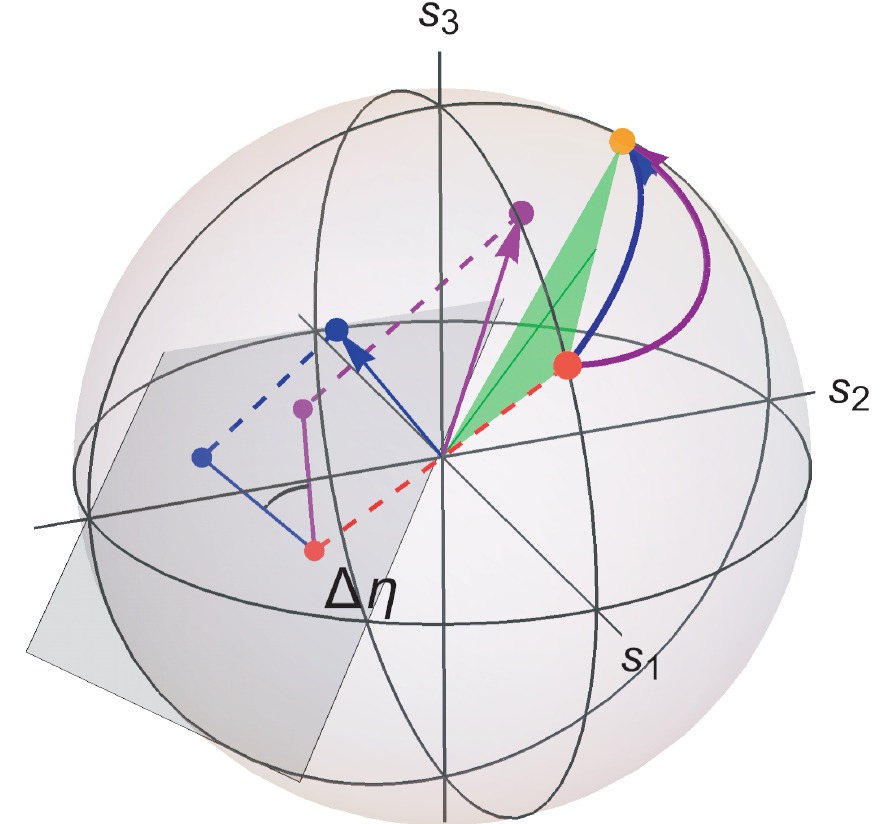
Geometric phases in optics and their application via optical elements with spatially-varying birefringence.

Measurements of polarization, spatial coherence, and applications in microscopy and metrology.
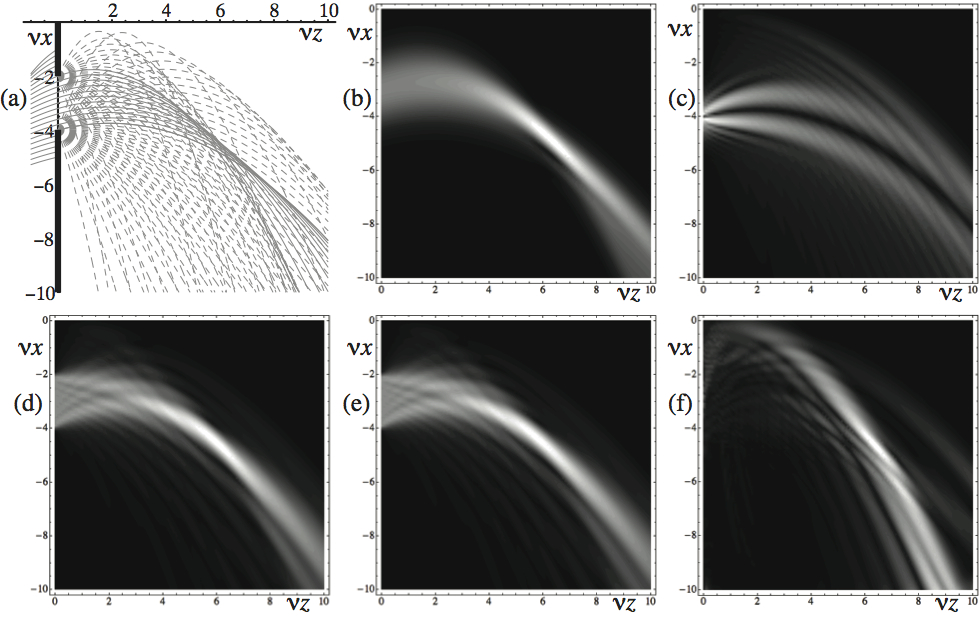 Mathematical connection between the ray and wave models of light, and methods for estimating wavefields from rays.
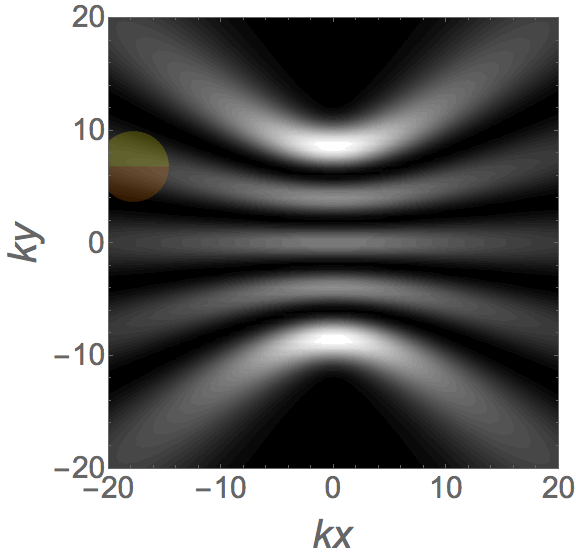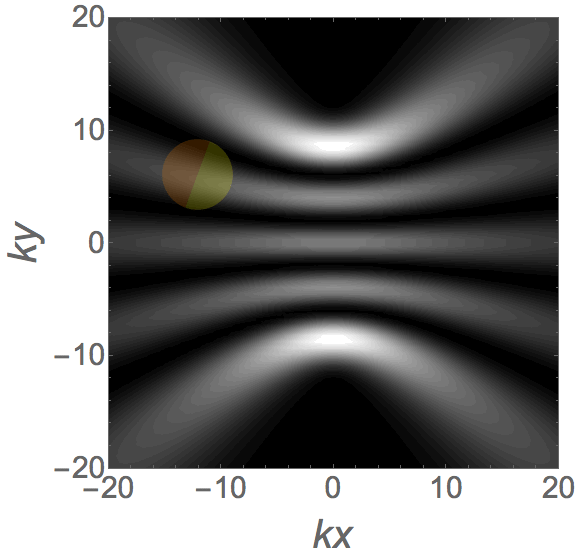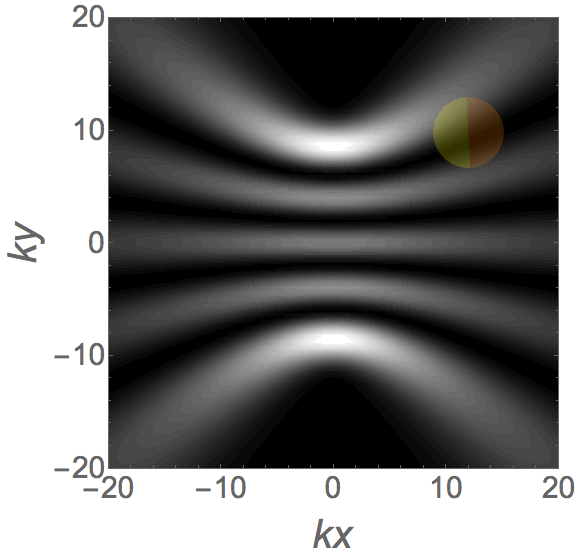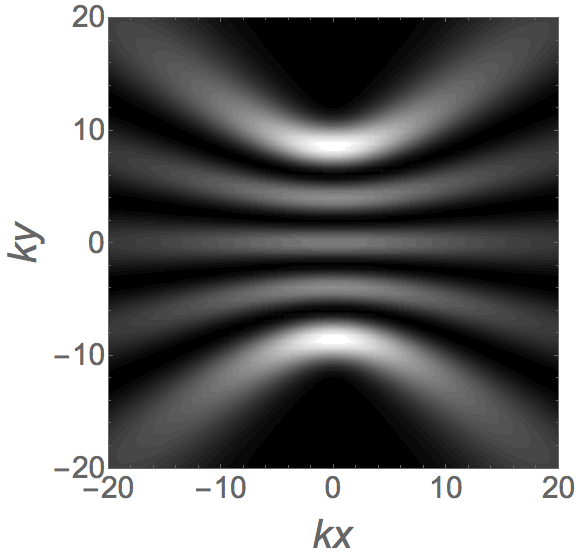 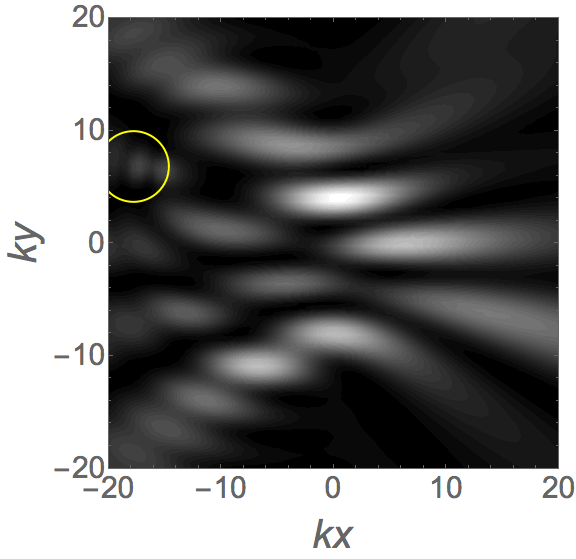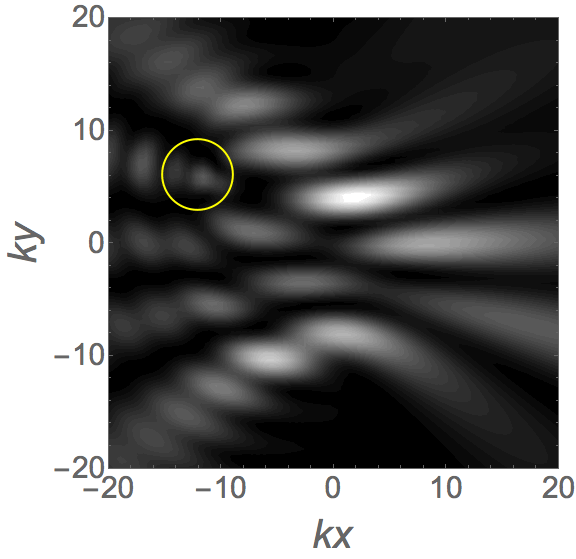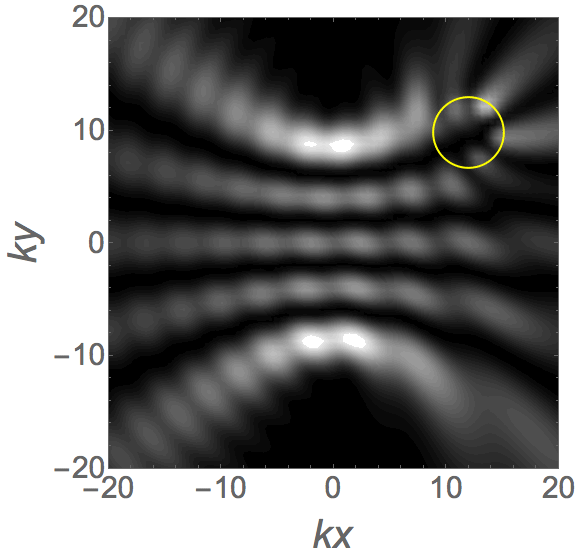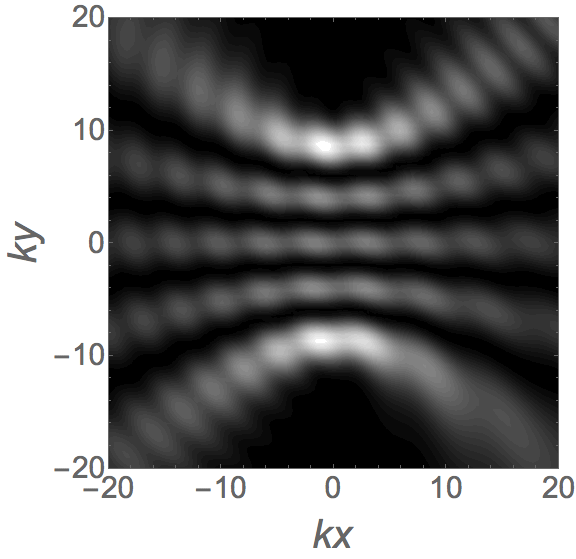
Analytical models for wave fields beyond the paraxial approximation. Fundamental relations related to focal properties, the effects of polarization, closed-form complete orthonormal basis expansions (nonparaxial generalizations of Laguerre-Gaussian beams), and generalizations of Mie theory describing the interaction with spherical scatterers. 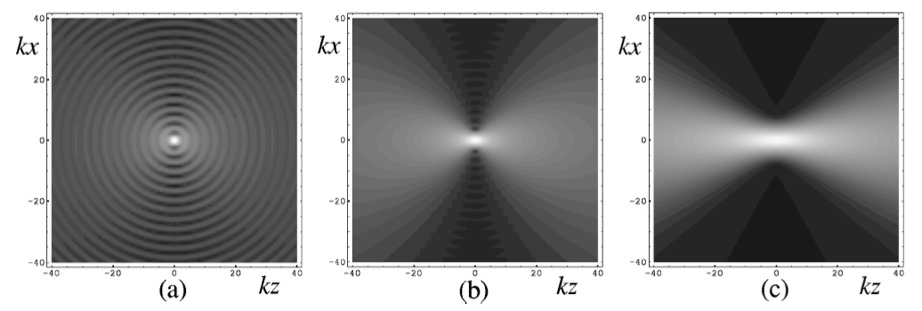 Measures of spread for periodic distributions (e.g., over a circle or a sphere) and the corresponding uncertainty relations they satisfy in several contexts. 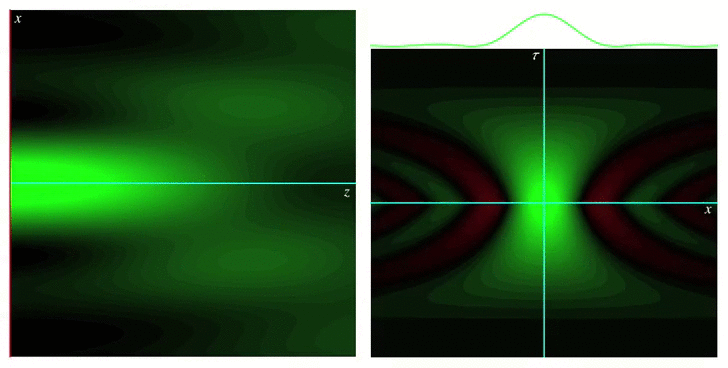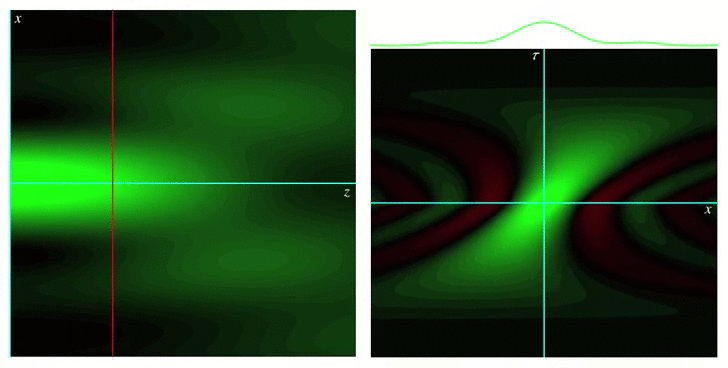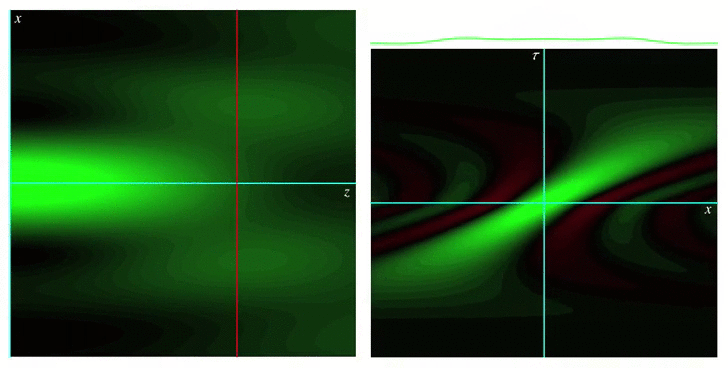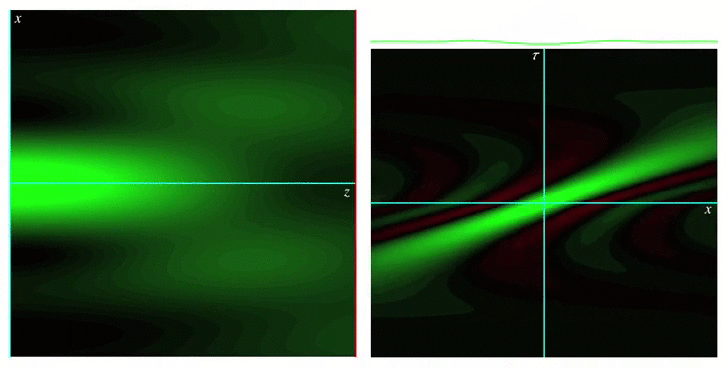 Phase space representations tailored for different physical situations, such as nonparaxial propagation of scalar and electromagnetic fields, diffraction effects, propagation of pulses through transparent media with arbitrary dispersion properties, and wave fields constrained to simple curved spaces.
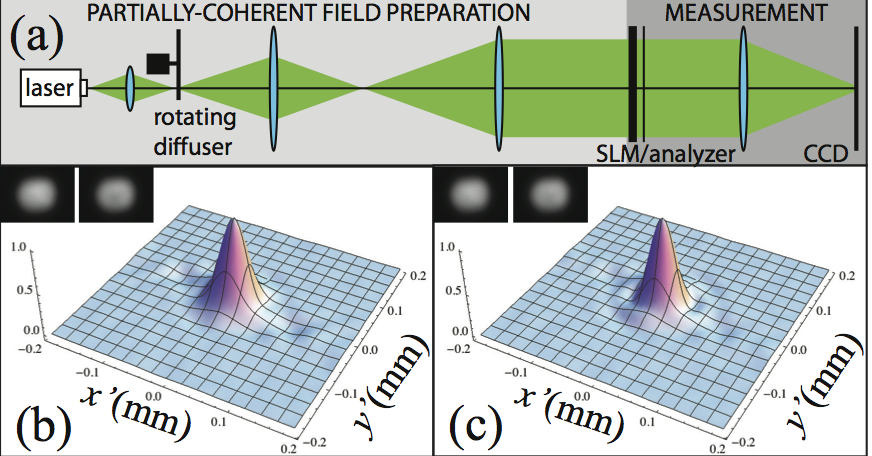 Theoretical description of partially coherent fields, and simple methods for measuring spatial coherence. 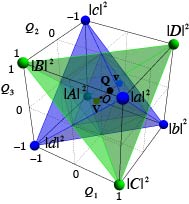 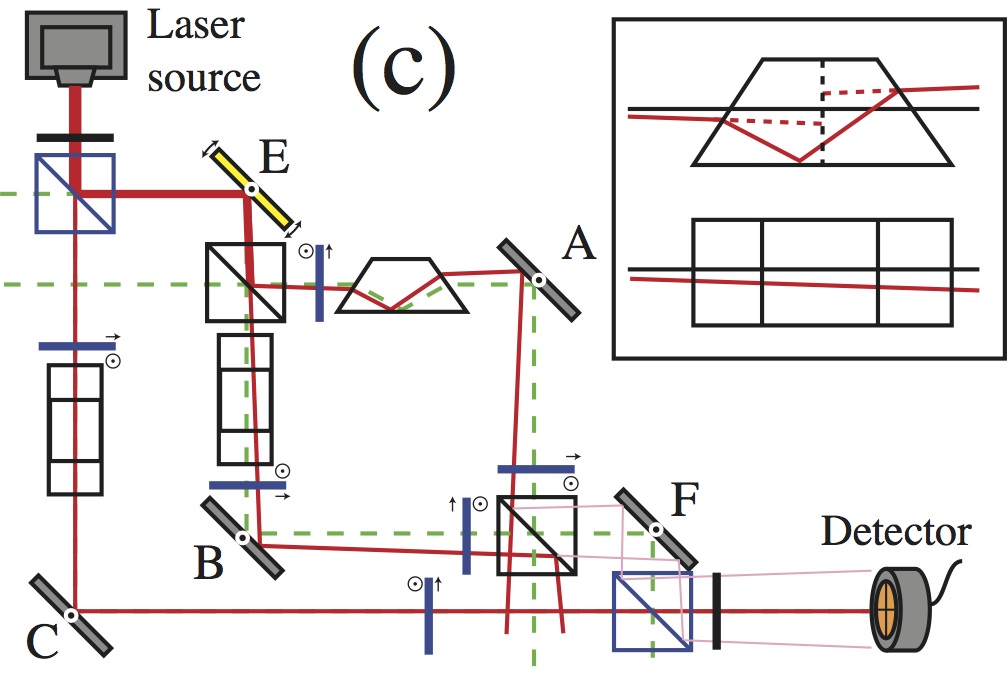 Measures of quantum entanglement and use of the weak measurement formalism.  Measures of performance of standard and freeform optical systems. Studies on exotic systems such as Maxwell fish eye lenses and refractive metasurfaces |